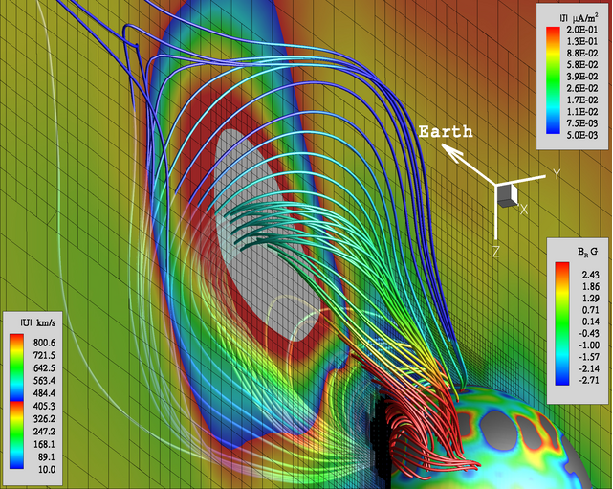
| 3D AMR simulation (using BATS-R-US) of the May 2, 1998
coronal mass ejection. The background solar wind was obtained using
solar magnetogram observations and the CME was initiated by rotating
and converging flows inside an active region. The 3D image shows the
CME 1 hour after eruption.
Solid lines are magnetic field lines; the false color code shows the
magnitude of the current density. The magnitude of the flow velocity
is shown on a translucent plane given by y=0. Values in excess of
1,000 km/s are blanked and shown in light grey. The inner sphere
corresponds to R=1 Rs; the color code shows the distribution of radial
magnetic field. Regions with radial field strength greater than 3
Gauss are blanked and appear in grey. The AMR grid is shown by thin
black lines on the plane.
|
BATS-R-US
|
|
The University of Michigan magnetohydrodynamic
(MHD) code BATS-R-US solves the MHD equations on a
block-adaptive grid. The code is based on a finite volume approach
with self-similar blocks. The parallel AMR solver was designed from
the ground up with a view to achieving very high performance on
massively parallel architectures. The hierarchical data structure and
self-similar blocks make domain decomposition easy and readily enable
good load-balancing, a crucial element for truly scalable
computing. The computational cells are embedded in regular structured
blocks. Starting with an initial mesh, adaptation is accomplished by
the dividing and refining of appropriate solution blocks or the
converse. Other features of the parallel implementation include the
use of FORTRAN 90 as the programming language and the message passing
interface (MPI) library for performing the interprocessor
communication. Use of these standards greatly enhances the
portability of the code and leads to very good serial and parallel
performance. The message passing is performed in an asynchronous
fashion with gathered wait states and message
consolidation. BATS-R-US nearly perfectly scales to 1,500
processors.
The present implementation of BATS-R-US supports Cartesian (x,y,z),
cylindrical (r,φ,z), or spherical (R or log(R),φ,θ)
coordinate systems. Both the cylindrical and spherical grids are
applicable for simulating toroidal plasma configurations. Cylindrical
grids one better suited for configurations in which the axis of
symmetry (or pole) is isolated from the simulation domain (such as
tokamak, stellarator, FRS). On the other hand, spherical coordinates
are favorable for spheromak-like configurations. The use of classical
toroidal coordinates for a simulation is challenging due to the
strongly stretched control volumes near the toroidal pole, but such
toroidal grids will be available at least for presenting and
visualizing the simulation results. A powerful parallel "coupling
toolkit" has been recently developed at Michigan that can efficiently
interpolate from one type of grid to another (like
cylindrical-to-toroidal).
|
|