Research Activities > Programs >
Incompressible Flows 2006>
Claude Bardos
|
|

CSIC Building (#406),
Seminar Room 4122.
Directions: home.cscamm.umd.edu/directions
|

Some Remarks on the Zero Viscosity Limit of Leray Solutions
Claude Bardos
Laboratoire Jacques-Louis Lions, University of
Paris VII
|
|
Abstract:
In this talk I will try to connect several known and
(and may be less known ) points of view on this very
classical problem. The simplest approach is the use
of the notion of dissipative solution, a very weak
notion of solution due to PL Lions and R. DiPerna.
In the absence of boundary any weak sequence of
Leray solutions of the Navier Stokes equation
converges (with fixed initial data and viscosity
going to zero) to a dissipative solution. Then,
whenever a smooth solution of the incompressible
Euler equation (with the same initial data) do
exist, this dissipative solution coincides with the
smooth one and the convergence is strong. What may
prevent this strong convergence to happen is (i) the
absence of smoothness of the solution of the Euler
equation which may be due to non regular initial
data (in 2D and 3D) or to the blow up phenomenon (an
unsolved issue ) in 3D.
(ii) The presence of boundary with a no-slip
boundary condition. I want to stress the latter case
because it is probably the most explicit situation
where a non-zero limit exists for the quantity
 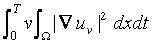
and where a dissipation of energy shows up. In the above situation, in particular
in the presence of smooth solution the dissipation of energy is related to the
fact that one has:
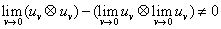
This difference may be approached with the introduction of the Wigner Measure. I
shall show that Wigner measures provide us with a natural extension of the
concept of energy spectrum, developed for the statistical theory of homogeneous
turbulence.
Finally I want to observe that the above convergence defect is related to blow
up in the Prandlt equations and to try to compare from the mathematical point of
view this problem with the Kelvin Helmholtz problem.
[LECTURE SLIDES]
|
|
|
